Vectors

Introduction to Vectors

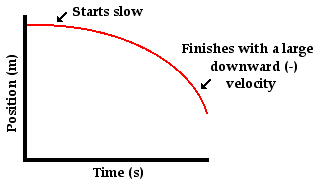
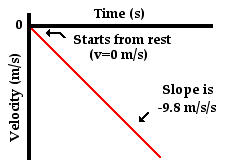
A study of motion will involve the introduction of a variety of quantities that are used to describe the physical world. Examples of such quantities include distance, displacement, speed, velocity, acceleration, force, mass, momentum, energy, work, power, etc. All these quantities can by divided into two categories - vectors and scalars. A vector quantity is a quantity that is fully described by both magnitude and direction. On the other hand, a scalar quantity is a quantity that is fully described by its magnitude. The emphasis of this unit is to understand some fundamentals about vectors and to apply the fundamentals in order to understand motion and forces that occur in two dimensions.

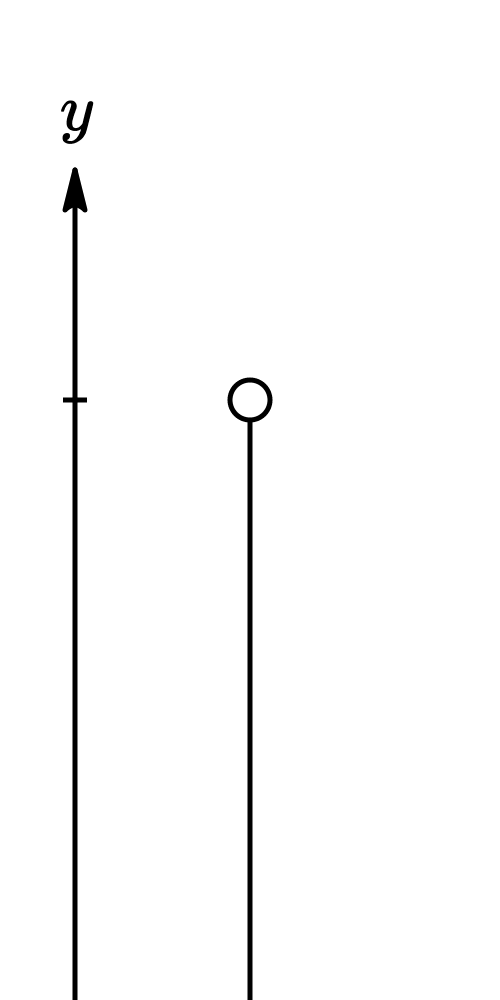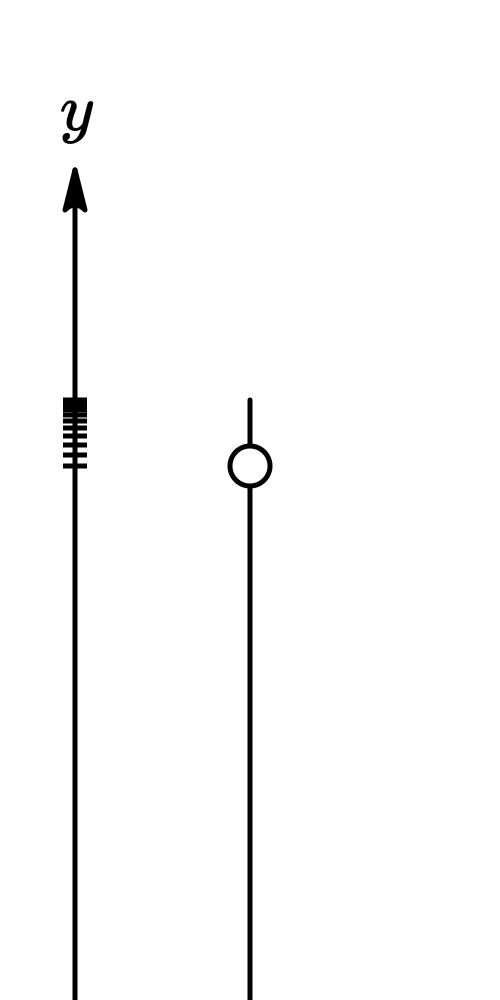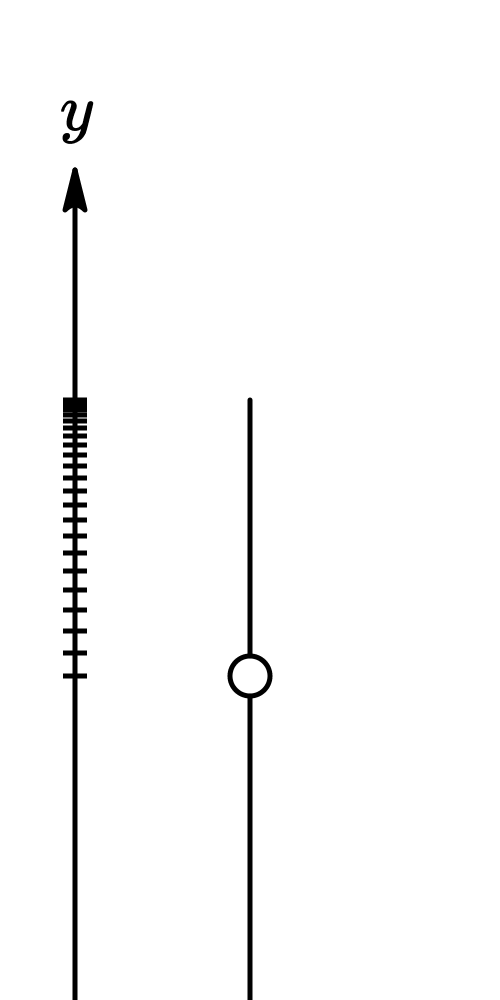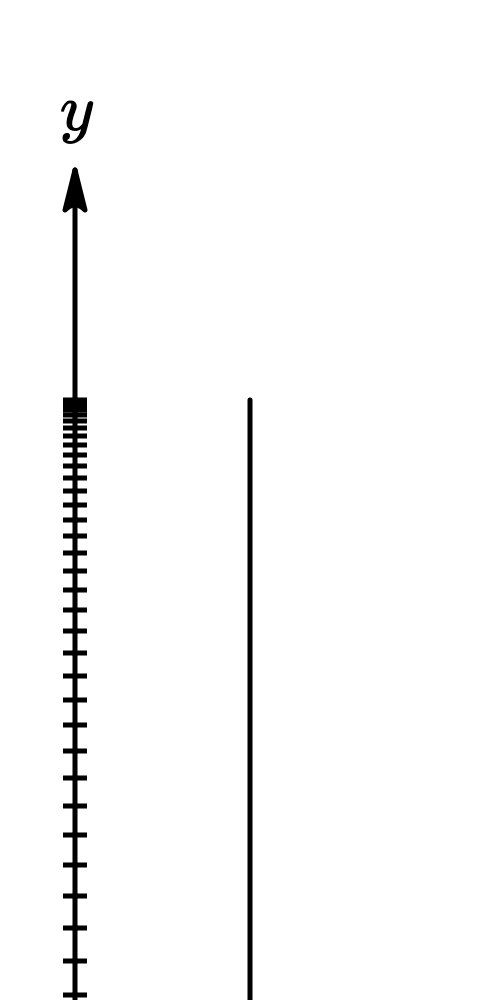
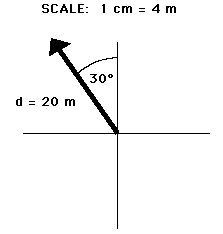Vector quantities are often represented by scaled vector diagrams. Vector diagrams depict a vector by use of an arrow drawn to scale in a specific direction. Vector diagrams were introduced and used in earlier units to depict the forces acting upon an object. Such diagrams are commonly called as free-body diagrams. An example of a scaled vector diagram is shown in the diagram in the right. The vector diagram depicts a displacement vector. Observe that there are several characteristics of this diagram that make it an appropriately drawn vector diagram.

• a scale is clearly listed
• a vector arrow (with arrowhead) is drawn in a specified direction. The vector arrow has a head and a tail.
• the magnitude and direction of the vector is clearly labeled. In this case, the diagram shows the magnitude is 20 m and the direction is (30 degrees West of North).

Vector Direction

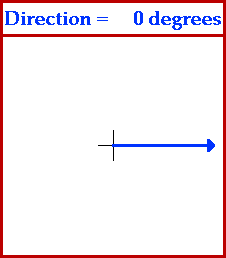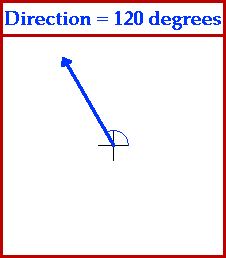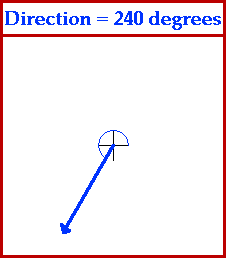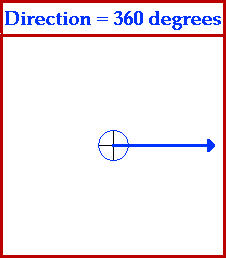
To fully describe a vector quantity, it is necessary to tell both the magnitude and the direction. For instance, if the velocity of an object were said to be 25 m/s, then the description of the object's velocity is incomplete; the object could be moving 25 m/s south, or 25 m/s north or 25 m/s southeast. To fully describe the object's velocity, both magnitude (25 m/s) and direction (e.g., south) must be stated.

In order for such descriptions of vector quantities to be useful, it is important that everyone agree upon how the direction of an object is described. The convention upon which we can all agree is sometimes referred to as the CCW convention - counterclockwise convention. Using this convention, we can describe the direction of any vector in terms of its counterclockwise angle of rotation from due east. The direction north would be at 90 degrees since a vector pointing east would have to be rotated 90 degrees in the counterclockwise direction in order to point north. The direction of west would be at 180 degrees since a vector pointing west would have to be rotated 180 degrees in the counterclockwise direction in order to point west. Further illustrations of the use of this convention are depicted by the animation below.

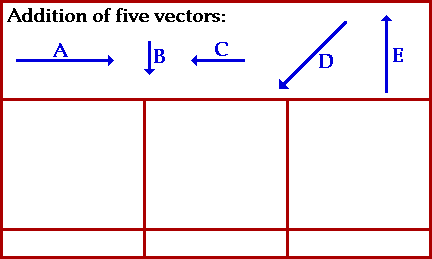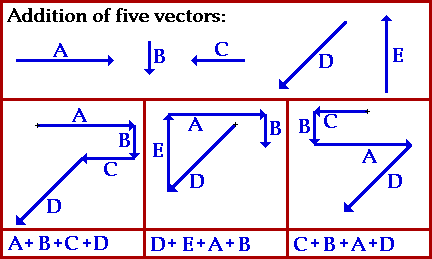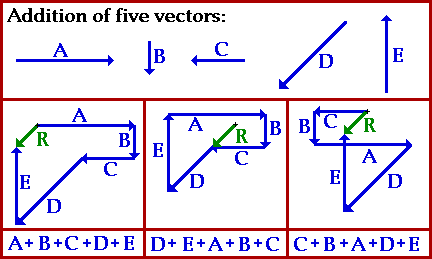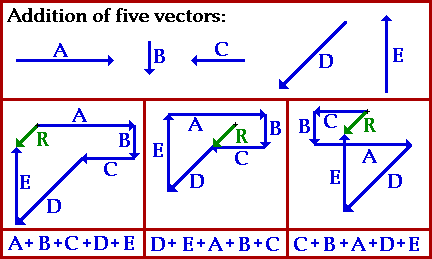
Vector Addition: The Order Doesn't Matter

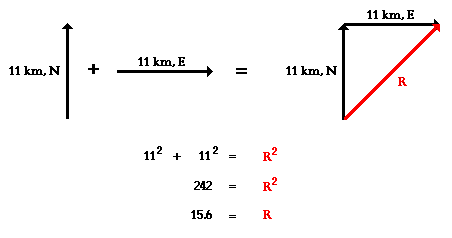
The summative result of two or more vectors can be determined by a process of vector addition. The most common method of adding vectors is the graphical method of head-to-tail addition. This method involves the selection of a scale (e.g., 1 cm = 5 km), and the subsequent drawing of each vector to scale in the specific direction. The tail of each consecutive vector begins at the head of the most recent vector. The resultant vector (the summative result of the addition of the given vectors) is then drawn from the tail of the first vector to the head of the last vector. The magnitude and direction of the resultant is then determined using a protractor, ruler, and the indicated scale.

The question often arises as to the importance of the order in which the vectors are added. For instance, if five vectors are added - let's call them vectors A, B, C, D and E - then will a different resultant be obtained if a different order of addition is used. Will A + B + C + D + E yield the same result as C + B + A + D + E or D + E + A + B + C? The animation below provides the answer. Observe the animation a couple of times and see what the answer is.

As you can see, adding vectors, like in mathematical addition, the order of the vector doesn't matter.

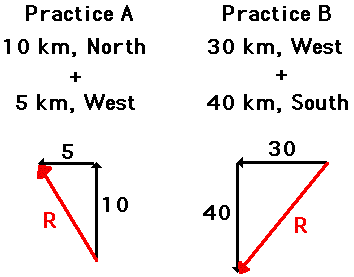
Sample Problems on Vectors

R² = (5)² + (10)²           R² = (30)² + (40)²

R² = 125                         R² = 2500

R = SQRT (125)             R = SQRT (2500)

R = 11.2 km                   R = 50 km

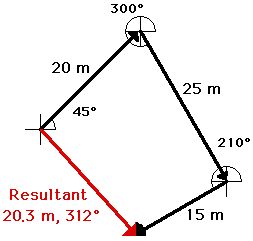
20 m, 45 deg. + 25 m, 300 deg. + 15 m, 210 deg.

SCALE: 1 cm = 5 m

Source: http://www.physicsclassroom.com/class/vectors/

Relating vectors to life: It is really of use in traveling-purposes especially when one is lost in the forest or dessert (I think) and you have no choice but to use your brain and find a compass. Well, reading a compass is somewhat related to analyzing 'counterclockwise convention' and  eventually to vectors. Bow.

Free Fall Motion

Introduction to Free Fall Motion

In air, a coin falls faster than a piece of paper. However, in a vacuum, they fall at the same rate. The difference, in air, is due to air resistance having a greater effect in light bodies than on heavier bodies. Thus, free fall is the motion of an object under the influence of gravity alone, neglecting air resistance.

For a long time, people believed that heavy bodies fall faster than light bodies, which was according to Aristotle . But according to legend, during the sixteenth century, Galileo Galilei disproved this by dropping a small iron and a large cannon ball from the Leaning Tower of Pisa. To the surprise of the onlookers, two balls almost reached the ground at the same time. (Physics at Work 1 by P. K. Tao, 1992)

Representing Free Fall by Graphs

A position versus time graph for a free-falling object is shown below.

Observe that the line on the graph curves. A curved line on a position versus time graph signifies an accelerated motion. Since a free-falling object is undergoing an acceleration (g = 9.8 m/s/s), it would be expected that its position-time graph would be curved. A further look at the position-time graph reveals that the object starts with a small velocity (slow) and finishes with a large velocity (fast). Since the slope of any position vs. time graph is the velocity of the object, the small initial slope indicates a small initial velocity and the large final slope indicates a large final velocity. Finally, the negative slope of the line indicates a negative (i.e., downward) velocity.

A velocity versus time graph for a free-falling object is shown below.

Observe that the line on the graph is a straight, diagonal line. As learned earlier, a diagonal line on a velocity versus time graph signifies an accelerated motion. Since a free-falling object is undergoing an acceleration (g = 9.8 m/s/s, downward), it would be expected that its velocity-time graph would be diagonal. A further look at the velocity-time graph reveals that the object starts with a zero velocity (as read from the graph) and finishes with a large, negative velocity; that is, the object is moving in the negative direction and speeding up. An object that is moving in the negative direction and speeding up is said to have a negative acceleration . Since the slope of any velocity versus time graph is the acceleration of the object , the constant, negative slope indicates a constant, negative acceleration. This analysis of the slope on the graph is consistent with the motion of a free-falling object - an object moving with a constant acceleration of 9.8 m/s/s in the downward direction. 

(http://www.physicsclassroom.com/Class/1DKin/U1L5c.cfm)

                                     

Diagrams on Free Falling Bodies

The Four Kinematic Equations on Free Fall

The symbols in the given equations have a specific meaning: 

the symbol Δy stands for the displacement; 

the symbol t stands for the time; 

the symbol g stands for the gravity= 9.8 m/s/s of the object; 

the symbol v_i stands for the initial velocity value; 

and the symbol v_f stands for the final velocity.

More likely 5% related to free fall